二回に渡りオランダの電力消費量データを見てきた. 今回はスマートメータの普及率を各州毎に見てみる.

data = df.groupby(['province', 'year']).agg({'smartmeters': 'sum', 'num_connections': 'sum'})
data = data.smartmeters/data.num_connections*100

for name in data.index.get_level_values(0).unique():
  plt.plot(data.xs(name, level='province'), label=name, marker='o')

plt.xlabel('Year')
plt.ylabel('Fraction of smart-meters [%]')
plt.legend()
plt.ylim(ymin=0)
plt.tight_layout()

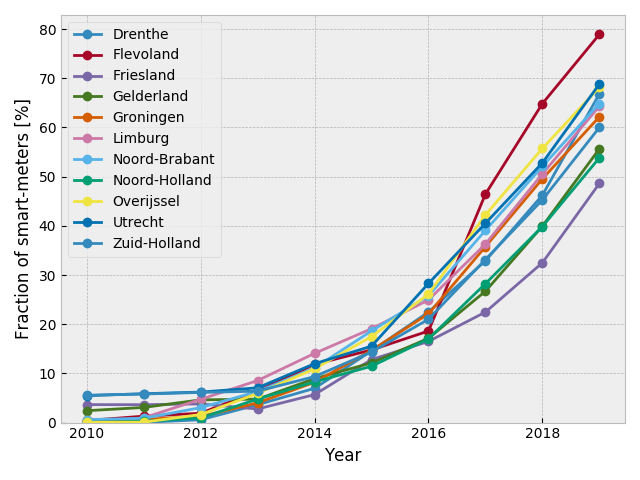最も普及が進んでいるのが Flevoland 州で最も遅れているのが Friesland 州. Friesland 州のデータを 中心値と成長率を変数とした logistic 曲線でフィットしてみる.

def logistic(x, midpoint, growth_rate, amplitude=100):
  return amplitude/(1. + np.exp(-growth_rate*(x - midpoint)))

name = 'Friesland'
X = data.xs(name, level='province').index
Y = data.xs(name, level='province').values
popt, pcov = scipy.optimize.curve_fit(logistic, xdata=X , ydata=Y , p0=[2016, 1])

Friesland 州のデータを表示して、フィットの結果を重ねる. フィットの結果は 2030年まで外挿し、1-$\sigma$ のエラーバンドを表示する.

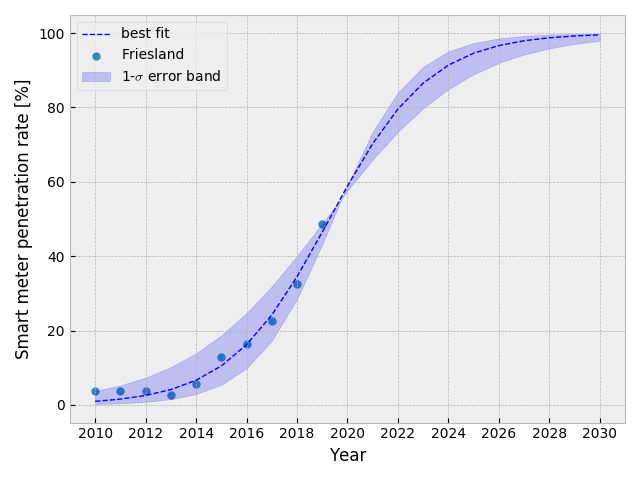
plt.scatter(X, Y,  marker='o', lw=0, label='Friesland') 
future = np.arange(2010, 2031)
plt.plot(future, logistic(future, popt[0], popt[1]), color='b', lw=1, ls='--', label='best fit')
y_lo = logistic(future, popt[0]-np.sqrt(pcov[0,0]), popt[1]-np.sqrt(pcov[0,0]))
y_hi = logistic(future, popt[0]+np.sqrt(pcov[0,0]), popt[1]+np.sqrt(pcov[0,0]))
plt.fill_between(future, y_lo, y_hi, alpha=0.2, color='b', label='1-$\sigma$ error band')
plt.xticks(future[::2], rotation=0)
plt.xlabel('Year')
plt.ylabel('Smart meter penetration rate [%]')
plt.legend()
plt.tight_layout()

普及率が 95%を超える年を予想してみる.

scipy.optimize.root_scalar(lambda x: 95. - 100/(1. + np.exp(-popt[1]*(x - popt[0]))), bracket=[2000,2100])

      converged: True
           flag: 'converged'
 function_calls: 14
     iterations: 13
           root: 2025.1606414014957

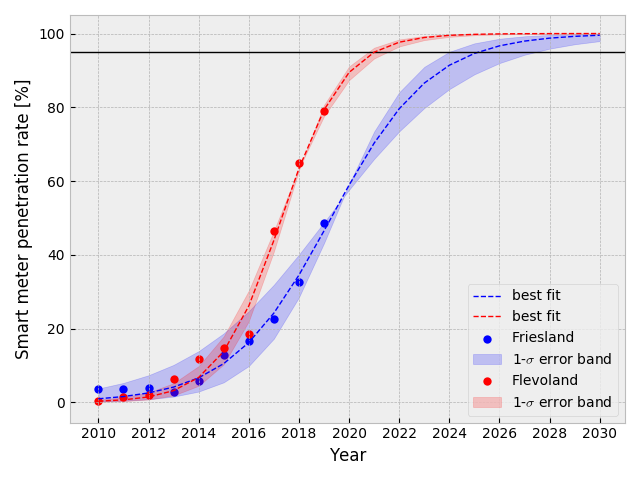
2025年の58日目 (二月下旬) に 95%を超えるとこのモデルでは予想される. 予想の 1-$\sigma$ 誤差は 3日程度. 同様にして、Flevoland 州で普及率が 95%を超えるのは 2021年の一月初旬と予想出来る. 最も普及が進んでいる州と最も普及が遅れている州とでは、凡そ4年の差が生じるとこのモデルでは予想される. 両州を重ねて表示すると以下のようになる.

---

Markov chain Monte Carlo (MCMC)

---

PyMC3 を使用して、上記と同様な regression 分析を行う.

中心値と成長率をそれぞれ正規分布で表す. 初期値には先ほどのフィットの結果を流用する.

import pymc3 as pm
import theano.tensor as tt

with pm.Model() as model:
  midpoint = pm.Normal("midpoint", mu=popt[0], tau=1./np.sqrt(pcov[0,0]), testval=0)
  growth_rate = pm.Normal("growth_rate", mu=popt[1], tau=1./np.sqrt(pcov[1,1]), testval=0)
  p = pm.Deterministic("p", 100./(1. + tt.exp(-growth_rate*(X.tolist() - midpoint))))

上記のモデルを用いて、MCMC を実行する.

with model:
  observed = pm.Logistic("logistic_obs", p, observed=Y.tolist())
  start = pm.find_MAP()
  step = pm.Metropolis()
  trace = pm.sample(220000, step=step, start=start)
  burned_trace = trace[200000::2]

中心値と成長率の posterior 分布.

pm.plots.plot_posterior(trace=trace["midpoint"])
pm.plots.plot_posterior(trace=trace["growth_rate"])

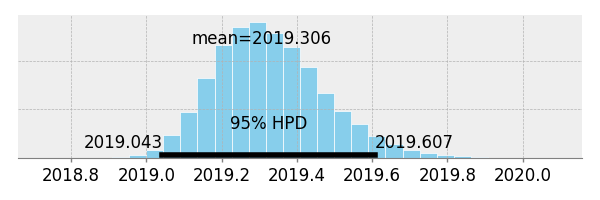
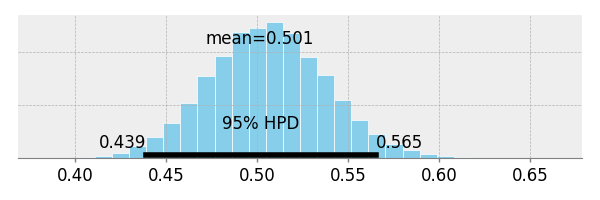
得られた結果を比較してみる. Bayesian の結果は、highest posterior density の 95%区間だが、Frequentist (SciPy fit) の結果は 1-$\sigma$ 区間 (68%). 比較の為、iminuit の minos error analysis の結果も比較する (2-$\sigma$ 区間).

	mean	low	high
midpoint [Freq.]	2019.282	2019.136	2019.427
growth rate [Freq.]	0.501	0.467	0.534
midpoint [Bays.]	2019.306	2019.043	2019.607
growth rate [Bays.]	0.501	0.439	0.565
midpoint [minos]	2019.282	2019.140	2019.431
growth rate [minos]	0.501	0.467	0.536

数字を見れば明らかだが Bayesian と minos の結果を重ねて表示してみると、Bayesian の方が既にデータがある年のエラーバンドは狭く、将来のエラーバンドが広くなっている. Bayesian の方が直感に近いが、MCMC を使用しているので、試行毎に得られる結果にバラツキがある.

qs = scipy.stats.mstats.mquantiles(p_t, [0.025, 0.975], axis=0)
plt.fill_between(t[:, 0], *qs, alpha=0.2, color="r")
plt.plot(t, mean_prob_t, lw=1, ls="--", color="r", label="average posterior probability")
plt.scatter(X, Y, color="k", s=50, alpha=0.5)

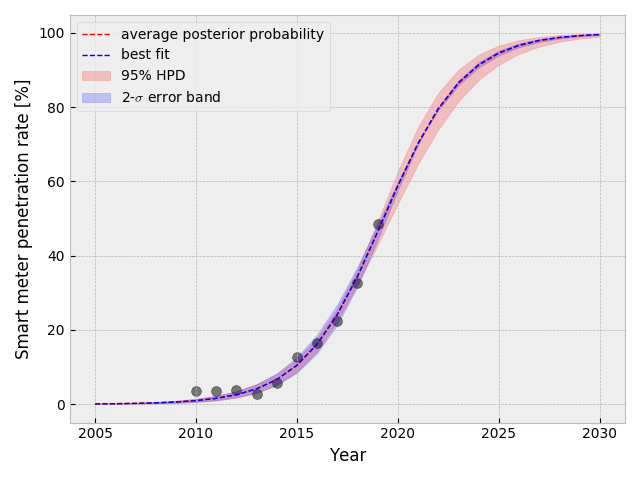以上、スマートメータの普及率を用いた統計分析を行った.