b) Predict RUL

---

The training data set includes the sequence of sensor readings until the time step at the engine failure, thus RUL can be calculated from the data set. The testing data set includes the sequence of sensor readings till the time step sometime before the engine failure. The RUL is available in the separate data set.

Set RUL for training set.

rul = pd.DataFrame(df_train.groupby('unit')['time'].max())
rul.reset_index(inplace=True)
rul.columns = ['unit', 'time_last']

train = pd.merge(df_train, rul, on='unit') 
train['rul'] = train['time_last'] - train['time']
train[train.unit==1][['rul', 'time_last', 'time']]  
train.drop(['time_last'], axis=1, inplace=True)

Check correlations of variables.

corr = train.corr()
print(corr['rul'].sort_values(ascending=False))

plt.figure()
mask = np.zeros_like(corr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
sns.heatmap(corr, mask=mask, annot=False, cmap='coolwarm')
plt.xticks(ticks=np.arange(len(corr.columns)), labels=corr.columns, fontsize=8, ha='left')
plt.yticks(ticks=np.arange(len(corr.columns)), labels=corr.columns, fontsize=8, ha='right')
plt.tight_layout()

phi          6.719831e-01
P30          6.572227e-01
W32          6.356620e-01
W31          6.294285e-01
unit         7.875253e-02
P2           1.561885e-14
T2           1.535649e-14
epr          1.414118e-14
farB        -3.799205e-15
mach        -1.947628e-03
altitude    -3.198458e-03
P15         -1.283484e-01
NRc         -3.067689e-01
Nc          -3.901016e-01
NRf         -5.625688e-01
Nf          -5.639684e-01
T30         -5.845204e-01
htBleed     -6.061536e-01
T24         -6.064840e-01
BPR         -6.426670e-01
T50         -6.789482e-01
Ps30        -6.962281e-01
time        -7.362406e-01
TRA                   NaN
Nf_dmd                NaN
PCNfR_dmd             NaN

Prepare training and validation set.

def get_train_val(df):
  units = df.unit.unique()
  np.random.seed(0)
  unit_train = np.random.choice(units, int(len(units)*0.8), replace=False)
  unit_test = np.array(list(set(units) - set(unit_train)))

  x_train = df[df.unit==unit_train[0]]
  y_train = df.rul[df.unit==unit_train[0]]
  for unit in unit_train[1:]:
    x_train = pd.concat([x_train, df[df.unit==unit]])
    y_train = pd.concat([y_train, df.rul[df.unit==unit]])

  x_val = df[df.unit==unit_test[0]]
  y_val = df.rul[df.unit==unit_test[0]]
  for unit in unit_test[1:]:
    x_val = pd.concat([x_val, df[df.unit==unit]])
    y_val = pd.concat([y_val, df.rul[df.unit==unit]])

  x_train.drop(['unit', 'time', 'rul'], axis=1, inplace=True)
  x_val.drop(['unit', 'time', 'rul'], axis=1, inplace=True)

  return x_train, x_val, y_train, y_val


x_train, x_val, y_train, y_val = get_train_val(train)

Linear Regression

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, explained_variance_score, r2_score

reg_lin = LinearRegression()
reg_lin.fit(x_train, y_train)
predictions = reg_lin.predict(x_val)
plt.figure()
plt.scatter(y_val, predictions, s=5, alpha=0.2)
plt.xlabel('RUL (true)')
plt.ylabel('RUL')

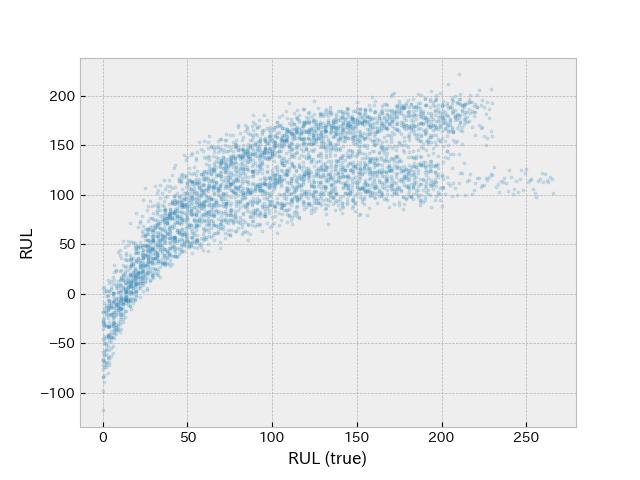
Two possible bands can be seen in RUL(true) vs prediction, which could be handled by more complex model or by adding more inputs.

For an engine degradation scenario an early prediction is preferred over late prediction. The asymmetric scoring function is given below.

\(s = \displaystyle\sum_{i=1}^{n} \exp{^{(-d/10)}} - 1\) for \(d \lt 0\)
\(s = \displaystyle\sum_{i=1}^{n} \exp{^{(d/13)}} - 1\) for \(d \ge 0\)

• s = score
• d = (estimated RUL) - (true RUL)
• n = number of engine units under test

Evaluate the model with some metrics.

def custom_loss(y_true, y_pred, weights=None):
  diff = np.array(y_pred, dtype=np.float) - np.array(y_true, dtype=np.float)
  mask = diff < 0.
  diff[mask] = np.exp(-diff[mask]*0.077) - 1.
  mask = diff >= 0.
  diff[mask] = np.exp(diff[mask]*0.1) - 1.
  return diff.sum()

predictions[predictions < 1] = 1
print('MSE', mean_squared_error(y_val, predictions))
print('R2', r2_score(y_val, predictions))
print('score', custom_loss(y_val, predictions))

MSE 1581.5952988817035
R2 0.5798722030677054
score inf